i. Observe o croqui e os resultados das Tabelas 2 e 3, obtidos a partir da análise qualitativa da ameaça e vulnerabilidade da sua escola. Com base nos resultados, este exercício propõe uma transformação de valores qualitativos em valores quantitativos e a utilização destes últimos para interpretação do risco interno da escola. Isto será feito a partir de um modelo matemático simples, a equação da reta.

ii. Pegue a Tabela 2 preenchida. Na coluna “vulnerabilidade”, ao lado dos círculos coloridos, atribua:

• Valor zero (0) a todas as respostas marcadas com a cor verde;
• Valor dois (2) a todas as respostas marcadas com a cor amarela;
• Valor cinco (5) a todas as respostas marcadas com a cor vermelha;

iii. Some todos os valores da coluna e preencha a caixa do “TOTAL”.

iv. Pegue a Tabela 2 preenchida. Na coluna “vulnerabilidade”, ao lado dos círculos coloridos, atribua:

• Valor zero (0) a todas as respostas marcadas com a cor verde;
• Valor dois (2) a todas as respostas marcadas com a cor amarela;
• Valor cinco (5) a todas as respostas marcadas com a cor vermelha;

v. Some todos os valores da coluna e preencha a caixa do “TOTAL”.

vi. A partir desses novos valores obtidos pela turma, e a ajuda do professor de matemática, considere:

• O valor total obtido da Tabela 2 = Y;
• O valor total obtido da Tabela 3 = X;

vii. Localize o ponto coordenado (X, Y) no plano cartesiano apresentado na figura abaixo:

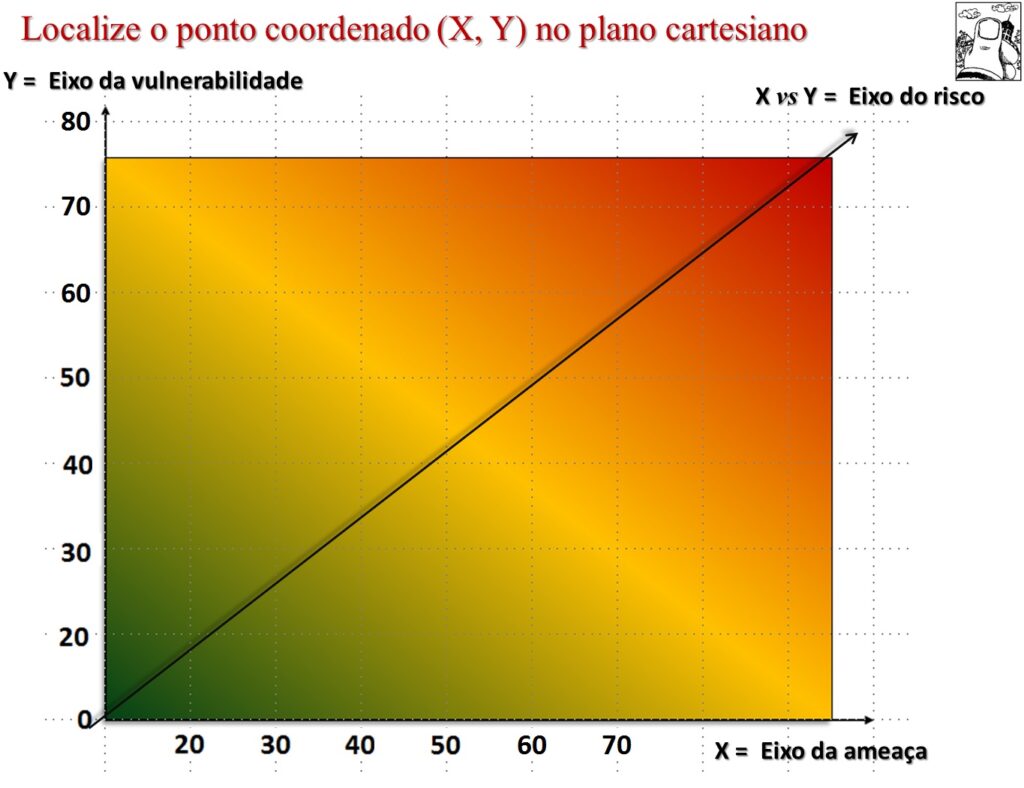
viii. Exercite a dedução da equação fundamental da reta que passa pela origem de coordenadas e pelo ponto coordenado (X, Y) localizado no plano cartesiano. Utilize o exercício do material de apoio. Exercício de geometria analítica: Dedução da equação fundamental da reta.

Questões para debate:

• Este exercício poderia ser adaptado a outras análises, de outros locais? Quais?
• Como se aplicaria a avaliação do risco da escola perante as ameaças externas identificadas na Tabela 1?